Industrial

Vertical Impact

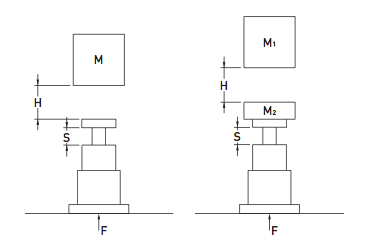
Design mass for buffer	Ep = Mg(H+S)
Maximum impact force
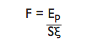
Design mass for buffe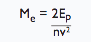r	or
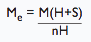
Initial Plunger Velocity
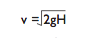
Multiple Mass Case:
Potential energy to be absorbed Maximum impact force	Ep = M1g (H+S) + M2gS
Maximum impact force
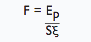
Initial Plunger Velocity
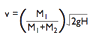
Buffer design Mass

Summary of notation

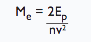
To avoid confusing conventions within calculations always use SI units in formulae then convert to more appropriate units if required.

Notation	Quantity	SI Unit
M	Mass of body	kg
M	Mass of body	kg
M	Mass of body	kg
Me	Buffer design mass	kg
Me	Freefall height	m
S	Buffer stroke	m
Ep	Potential energy	J
v	Velocity	m/s
F	Maximum Impact force	N
m/s2	Acceleration due to gravity	g
n	Number of buffers in parallel	-
ξ	Efficiency	-

Worked example

Eg. Consider a body of mass (M₁) = 22000kg (22 tonnes) / free falling onto another body of mass (M₂) 3000kg (3 tonnes) supported by a buffer.The free fall height (H) being 0.15m. A typical example of this being in catch gear buffers for mine cages where 4 Type 4-114mm stroke buffers are used; this is a multiple mass case.

To find the equivalent energy absorbed:
E_p = M₁ g (H+S) + M₂ g S = (22000).(0.15+0.114) x 9.81 + 3000 x 9.81 x 0.114 = 60331.5J = 60.3315kJ

To find the maximum impact end force:

F = 661529.6N = 661.5296 kN

To find the equivalent mass for metering pin selection:
Initial plunger velocity

By selecting a Type 4 buffer with a dynamic capacity of 1000 kN these requirements are met.Therefore select metering pin code 05 for masses up to 20000kg (20 tonnes).