Industrial

Rotational Impact

Kinetic energy to be absorbed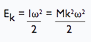
Energy due to drive force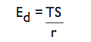
Total energy to be absorbed	ET = Ek + Ed
Maximum impact force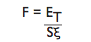
Design mass for buffer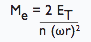

Summary of notation

To avoid confusing conventions within calculations always use SI units in formulae then convert to more appropriate units if required.

Notation	Quantity	SI Unit
M	Mass of body	kg
Me	Buffer design mass	kg
S	Buffer stroke	m
K	Radius of gyration	m
Ek	Kinetic energy	J
Ed	Energy due to drive force	J
Et	Total energy	J
ω	Angular velocity	rad/s
I	Moment of inertiaa	kg.m2
T	Torque	Nm
F	Impact force	N
N	Number of buffers in parallel	–
ξ	Efficiency	-

Worked example

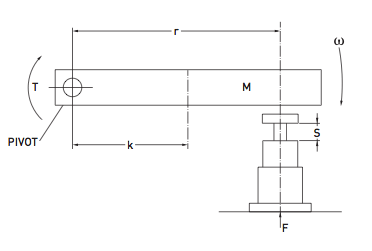
Eg. Consider a swing bridge, having a moment of inertia (I) of 7500000 kgm2, buffer arm radius (r) 8m, angular velocity (ω) of 0.174 rad/sec and a driving torque (T) of 1500000 Nm. Using 2 buffers.

To find the energy to be absorbed:

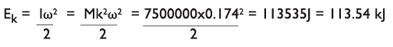
Let us select a Type 4 with 114mm stroke:

Total energy to be absorbed:
Therefore E_T = E_k + E_d = 113535 + 21375 = 134910 J = 134.91 kJ

To find the maximum impact force:

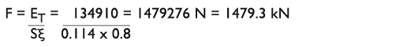
§To find the equivalent mass for metering pin selection:

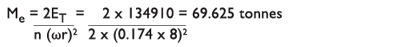
Therefore select metering pin code 08 for masses up to 80000kg (80 tonnes).